5.3 Representación matricial de una transformación lineal.
5.3. REPRESENTACIÓN MATRICIAL DE UNA TRANSFORMACIÓN LINEAL
DEFINICIÓN
Su definición
Sean V y W dos espacios vectoriales de dimensión n y m, respectivamente, y sea
T: V→W una transformación lineal, entonces existe una
matriz A de orden m × n llamada matriz de
transformación o representación matricial de T que satisface T (v) = Av para
toda v en V.
Representación
Matricial de una transformación R3 en R4
Si se tiene
una transformación T: R3 → R4 dada por
La T
representa la transformación, que será representada por AT, mientras
que la matriz a su lado representa el vector original. El resultado es la
transformación realizada. Para poder representarla de forma matricial lo que se
debe obtener es la matriz de transformación. Ya que a la vez se obtiene,
se pueden determinar otros datos como el núcleo y la imagen de la
transformación.
Para este
caso utilizando el resultado de la transformación, se puede determinar
fácilmente la matriz de transformación, separando el vector original y
determinando las operaciones que se realizaron.;
Y su
representación quedaría como la matriz de trasformación multiplicando al vector
original para dar como resultado a la transformación:
EJEMPLOS
·
Ejemplo 1.
Encuentre la representación matricial de la transformación lineal
T de endefinida por
Aplicamos T a
los vectores base de
Entonces la matriz AT es
·
Ejemplo 2.
En
el ejemplo 1 se utilizó la base canónica para construir la matriz de representación de la
transformación lineal
Ahora se utilizará la base.
Entonces la nueva matriz de
transformación queda:
·
Ejemplo 3.
Encuentre
la representación matricial AT de la
transformación lineal T definida
por
Aplicamos T a
los vectores base de ![]() :
:
Entonces la
matriz de
transformación es
·
Ejemplo 4.
Encuentre
la representación matricial AT de la
transformación lineal T definida por
Aplicamos
la transformación a los vectores base de
Entonces la matriz de transformación es.
IMÁGENES
VÍDEOS DE APOYO





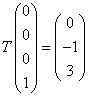
















Hola, tengo dos preguntas:
ResponderBorrar¿Para poder representar de forma matricial una matriz que se debe obtener?
¿Cuándo se obtiene la matriz de transformación que se puede determinar?
Para la primera pregunta se debe obtener una matriz de transformación.
BorrarY para la segunda se pueden determinar varios datos como el núcleo y la imagen de la transformación.
¿Cuando existe una matriz A de orden m x n como se le llama?
ResponderBorrarSe le llama matriz de transformación o representación matricial.
Borrar¿ Que representa la T y a por que será representada?
ResponderBorrarLa T representa la transformación, que será representada por AT.
Borrar¿como se puede determinar la matriz de transformación?
ResponderBorrarSe determina separando el vector original y determinando las operaciones que se realizaron.
Borrar¿como quedaría la representación de un matriz?
ResponderBorrarLa representación quedaría como la matriz de transformación multiplicando al vector original para dar como resultado a la transformación.
Borrar