5.4 Aplicación de las transformaciones lineales: reflexión, dilatación, contracción y rotación.
5.4 Aplicación de las transformaciones lineales: reflexión, dilatación, contracción y rotación.
4. Aplicación de las transformaciones lineales.
En primer lugar, una transformación lineal es una función. Por ser función, tiene su dominio y su co-dominio, con la particularidad de que éstos son espacios vectoriales. Tenemos dos espacios vectoriales V y W, y una función que va de V a W. Ósea, una regla de asignación que transforma vectores de V en vectores de W. Pero no toda función que transforme vectores de V en vectores de WW es una transformación lineal. Debe cumplir ciertas condiciones:
F: V→WF: V→W es una transformación lineal si y sólo si:
• F(u+v) =F(u)+F(v) ∀u, v∈VF(u+v) =F(u)+F(v) ∀u, v∈V
• F(k*v) =k*F(v) ∀v∈V, ∀k∈RF(k*v) =k*F(v) ∀v∈V, ∀k∈R
4.1. Reflexión.
Cuando un conjunto de puntos dados es graficado desde el espacio euclidiano de entrada a otro de manera tal que este es isométrico al espacio euclidiano de entrada, la llamamos reflexión del conjunto de puntos dados. También se realiza con respecto a la matriz, en tal situación la matriz de salida es llamada la matriz de reflexión. La reflexión es realizada siempre con respecto a uno de los ejes, sea el eje x o el eje y. Esto es como producir la imagen espejo de la matriz actual.
4.2. Dilatación.
Al igual que en la reflexión, se pueden expandir los puntos dados en una dirección particular. La expansión se realiza habitualmente para un cierto grado. Es como realizar una operación de multiplicación de los elementos del conjunto de puntos dados con un término escalar hacia la dirección donde tiene que ser expandido. Sea para un punto (2, 3) si el grado de expansión 2 es la dirección de y, entonces el nuevo punto obtenido es (2, 6).
4.3. Contracción.
La contracción es el procedimiento inverso de la expansión. Aquí el punto es contraído en un determinado grado hacia una dirección dada. Sea el punto de entrada (4, 8) y este debe ser contraído para el grado dos en la dirección de x entonces el nuevo punto resulta ser (2, 8).
4.4. Rotación.
El término rotación tiene dos significados, pues la rotación de un objeto puede ser realizada con respecto al eje dado o al eje mismo. La rotación se realiza para un cierto grado el cual es expresado en forma de un ángulo. Asimismo, la rotación puede realizarse en la dirección de las manecillas del reloj, o inverso a las manecillas del reloj.
Videos de apoyo.
Elaborado por.
José Manuel Zambrano Luna.
Dulce María Rangel Alcalá.
Bradley William Dávalos Espinoza.
Luis Felipe Hernandez Soto.
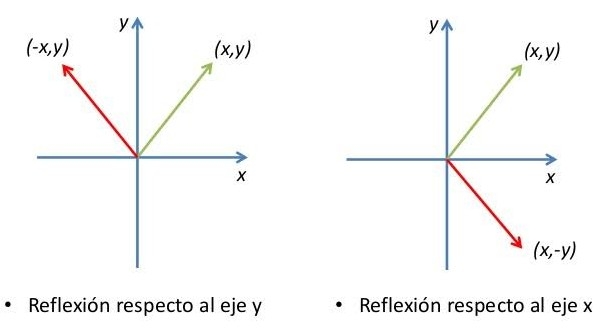





¿Para que sea de reflexión, debe mantenerse el mismo ángulo en un eje distinto como si fuera un espejo?
ResponderBorrarAsí es, si la línea o recta se encuentra en el cuadrante I, se refleja en otro cuadrante dependiendo si es con el eje y o el eje x.
BorrarSi queda con el eje y la línea se refleja de un lado a otro, si es con el x de arriba a abajo.
¿Entonces para que sea dilatación se multiplica el valor de y, pero el de x se mantiene?
ResponderBorrarEfectivamente, así la línea o recta crece en el eje de las y, pero mantiene su distancia respecto al de las x.
Borrar¿Cómo sé cuándo es de rotación?
ResponderBorrarUna transformación lineal por rotación es aquella en la que la recta pasa a otro cuadrante cambiando su ángulo sin modificar su forma, como una aguja en sentido de las manecillas del reloj.
Borrar¿Cuál es la diferencia entre el de rotación y reflexión?
ResponderBorrarEl de rotación gira la línea a través de los cuadrantes como un reloj, mientras que el de reflexión refleja la línea como si de un espejo se tratase.
Borrar¿Cual es la diferencia entre el de contracción y dilatación?
ResponderBorrarLa transformación lineal de dilatación muestra un crecimiento en la recta, mientras que el de contracción es una reducción de la misma.
Borrar
ResponderBorrar¿En el de dilatación, cuál es el valor a cambiar?
Generalmente el valor de y, para que así la recta crezca en el eje y sin aumentar en el de x.
Borrar